Nel settore delle ricerche di mercato, il margine di errore è un indicatore molto importante che determina quanto i risultati ottenuti da un campione rappresentino fedelmente la popolazione generale. Questo concetto è fondamentale per le aziende che si affidano a dati quantitativi per guidare le loro decisioni strategiche. Ma andiamo nel dettaglio e scopriamo di più sul significato del margine di errore.
Margine di errore: di che cosa si tratta?
Il margine di errore indica l’intervallo entro cui ci si aspetta che i risultati di un sondaggio differiscano dai veri valori della popolazione totale. Serve a misurare l’incertezza associata ai risultati di un sondaggio ed è direttamente influenzato dalla dimensione del campione e dalla variabilità delle risposte.
L’importanza nel contesto aziendale
Per le aziende, comprendere il margine di errore aiuta a:
- Valutare la precisione dei dati: Assicurarsi che le decisioni siano basate su dati affidabili.
- Supportare decisioni strategiche: Fornire una base solida per le strategie di marketing, sviluppo prodotto e espansione di mercato.
- Mitigare i rischi: Ridurre il rischio di decisioni basate su interpretazioni errate dei dati raccolti.
Come si calcola?
Formula standard
Il margine di errore si calcola usando la formula:
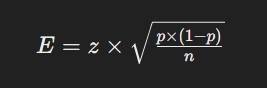
dove:
Eè il margine di errore,zè il valore z per il livello di confidenza scelto (ad esempio, 1.96 per il 95%),pè la proporzione della caratteristica di interesse nel campione,nè la dimensione del campione.
Esempi di calcolo
Sondaggio di Opinione: Un sondaggio su 1500 persone mostra che il 40% supporta una nuova legge. Il margine di errore per un livello di confidenza del 95% sarebbe calcolato come segue:
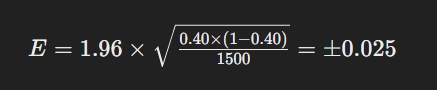
Questo risultato indica che il vero supporto nella popolazione può variare dal 37.5% al 42.5%.
Altre formule
Oltre alla formula standard, esistono altre formule e metodi per calcolare il margine di errore a seconda del tipo di dati e del contesto specifico dell’indagine:
- Correzione per la Popolazione Finita (FPC): Quando il campione è una parte significativa della popolazione totale, si applica la correzione per la popolazione finita:
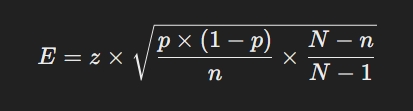
dove è la dimensione della popolazione totale. - Distribuzione t di student: Per campioni piccoli o quando la varianza della popolazione è sconosciuta, si utilizza la distribuzione t di Student invece della distribuzione normale.
- Margine di error per medie: Quando si tratta di calcolare il margine di errore per una media, la formula è:
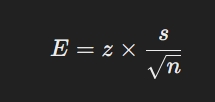
dove s è la deviazione standard del campione. - Margine di errore asimmetrico: In alcuni casi, specialmente con proporzioni vicine a 0 o 1, il margine di errore può non essere simmetrico. Tecniche di bootstrapping possono essere utilizzate per ottenere stime più accurate.
Queste formule alternative permettono di adattare il calcolo del margine di errore a una varietà di situazioni, migliorando l’accuratezza e l’affidabilità delle analisi statistiche nelle ricerche di mercato.
Fattori che influenzano il margine di errore
Dimensione del campione
Un campione più grande riduce il margine di errore, aumentando la precisione dei risultati. È essenziale bilanciare il costo di un campione più ampio con il beneficio di una maggiore precisione.
Proporzione di risposta
La variabilità delle risposte influenza il margine di errore; proporzioni vicino al 50% tendono a massimizzare il margine di errore, mentre proporzioni vicino a 0% o 100% lo minimizzano.
Quando si applica?
Il margine di errore non è solo una cifra teorica; ha applicazioni pratiche significative nel mondo del business, specialmente nelle seguenti aree:
- Lancio di nuovi prodotti: Prima di introdurre un nuovo prodotto sul mercato, le aziende utilizzano ricerche di mercato per testare l’accettazione del prodotto. Un margine di errore ben calcolato aiuta a determinare se il supporto apparente per il prodotto è statisticamente significativo o potenzialmente casuale.
- Segmentazione del mercato: Il margine di errore aiuta a identificare e a comprendere meglio i segmenti di mercato specifici. Questo è cruciale per targetizzare efficacemente le campagne di marketing e ottimizzare le strategie di vendita.
- Monitoraggio della soddisfazione del cliente: Le aziende spesso conducono sondaggi per misurare la soddisfazione dei clienti. Interpretare questi dati attraverso il prisma del margine di errore permette di capire meglio la fedeltà del cliente e la qualità del servizio.
Considerazioni metodologiche
Livello di confidenza e valore di z
Il livello di confidenza scelto influisce direttamente sulla grandezza del margine di errore: un livello di confidenza più alto richiede un valore di z più grande, aumentando così il margine di errore. Per esempio, un livello di confidenza dell’99% richiederebbe un valore di z di circa 2.58, espandendo l’intervallo di incertezza.
Effetto della proporzione p
La proporzione pp ha un impatto cruciale sul calcolo del margine di errore. Quando pp è vicino a 0.5, il prodotto p×(1−p)p \times (1-p) è massimizzato, il che aumenta il margine di errore. Questo è particolarmente rilevante quando si interpretano risultati di sondaggi su temi divisivi dove le opinioni possono essere quasi equamente divise.
Il margine di errore e le ricerche di mercato: Case History

Il margine di errore gioca un ruolo chiave in diversi settori e contesti, dimostrando la sua importanza nel fornire risultati accurati e affidabili. Ecco alcuni esempi concreti di come il margine di errore è stato utilizzato per influenzare decisioni significative nel mondo reale.
Settore sanitario: studi clinici
In uno studio clinico condotto per testare l’efficacia di un nuovo farmaco per il trattamento del diabete, un campione di 2.000 pazienti è stato selezionato. I risultati hanno mostrato che il 60% dei pazienti ha risposto positivamente al trattamento. Con un margine di errore di ±2%, i ricercatori possono affermare con un livello di confidenza del 95% che il vero tasso di efficacia del farmaco nella popolazione generale varia tra il 58% e il 62%. Questo intervallo di confidenza ha aiutato l’azienda farmaceutica a prendere decisioni informate riguardo alla produzione e alla commercializzazione del farmaco.
Industria dei media: sondaggi elettorali
Durante le elezioni presidenziali, un noto istituto di sondaggi ha rilevato che il candidato A godeva del 51% del supporto degli elettori, con un margine di errore di ±3%. Questo significa che il supporto effettivo potrebbe variare dal 48% al 54%, lasciando aperta la possibilità che il candidato B potesse effettivamente avere una quota di supporto simile o superiore a quella di A. Questi dati hanno influenzato le strategie dei candidati e le aspettative dei media riguardo all’esito delle elezioni.
Settore alimentare: ricerche di mercato sule preferenze dei consumatori
Un’azienda alimentare ha condotto un sondaggio per determinare la preferenza dei consumatori tra due nuovi gusti di snack. Il sondaggio ha coinvolto 1.500 consumatori e ha mostrato una leggera preferenza per il gusto A (55% contro 45%). Tuttavia, con un margine di errore di ±4%, l’azienda ha capito che non c’era una differenza significativa tra le preferenze per i due gusti, il che ha portato alla decisione di lanciare entrambi i prodotti sul mercato.
Tecnologia: valutazione della soddisfazione del cliente
Un’azienda tecnologica ha misurato la soddisfazione dei clienti dopo il rilascio di un nuovo software. Con un margine di errore di ±5%, hanno scoperto che il 70% dei clienti era soddisfatto del prodotto. Questo ha fornito una base solida per il team di sviluppo per continuare a migliorare il software, garantendo che le future versioni del prodotto rispondano ancora meglio alle esigenze degli utenti.
Impatto sociale: valutazione di programmi di aiuto
Un’organizzazione non profit che lavora per ridurre la povertà ha condotto sondaggi per valutare l’efficacia dei suoi programmi. Con un margine di errore di ±3%, i risultati hanno mostrato che il 62% delle famiglie beneficiarie ha riportato un miglioramento nelle loro condizioni di vita. Questi dati hanno aiutato l’organizzazione a ottimizzare i suoi sforzi e a garantire che i fondi vengano investiti nei programmi più efficaci.
Possiamo, dunque, affermare che il margine di errore è più di un semplice numero statistico; è un elemento vitale che influisce su decisioni di vasta portata in vari settori. Comprendere e calcolare accuratamente il margine di errore permette alle aziende e alle organizzazioni di prendere decisioni basate su dati affidabili, riducendo il rischio e aumentando la probabilità di successo nelle loro iniziative.
Chiedi all’esperto: collabora con Business Intelligence Group
Sei interessato a garantire che le tue decisioni aziendali siano guidate da dati accurati e affidabili? Parla con gli esperti di BIG.
Collaborare con noi significa assicurarti che ogni decisione sia supportata da analisi di mercato all’avanguardia e personalizzate per le tue specifiche esigenze. Che tu stia lanciando un nuovo prodotto, esplorando nuovi mercati o misurando la soddisfazione dei clienti, abbiamo gli strumenti e l’expertise per potenziare la tua presa di decisioni.
Contattaci oggi stesso per scoprire come possiamo trasformare i tuoi dati in decisioni potenti e di successo. Perché quando si tratta di dati, ogni percentuale e ogni punto percentuale contano. Business Intelligence Group: il tuo partner strategico nell’analisi dei dati.




